|
Меню Символика (Symbolics) Mathcad. Пункт Преобразования
вернуться на главную страницу можно, воспользовавшись ссылкой.
Интегральные преобразования по определению ставят в соответствие некоторой функции f (х) другую функцию от другого аргумента F(w). Причем это соответствие f(x) -» F(co) задается интегральной зависимостью. Символьный процессор Mathcad позволяет осуществлять три вида интегральных преобразований функций:
преобразование Фурье,
преобразование Лапласа
Z-преобразование. Наряду с прямыми преобразованиями имеется возможность совершать любое из этих трех обратных преобразований, т. е. F(w)->f (x) .
Аналитически все интегральные преобразования выполняются аналогично символьному интегрированию. Для вычисления преобразования выражения выделяется переменная, по которой будет осуществляться преобразование, и затем выбирается соответствующий пункт меню. Преобразования с применением оператора символьного вывода используются с одним из соответствующих ключевых слов, вслед за которым требуется указать имя нужной переменной. Приведем примеры символьного расчета каждого из трех интегральных преобразований.
Преобразование Фурье представляет функцию f (х) в виде интеграла по гармоническим функциям, называемого интегралом Фурье.
Аналитический расчет преобразования Фурье при помощи меню показан на рис. 1, для чего используется команда меню Symbolics / Transform / Fourier (Символика / Преобразование / Фурье).
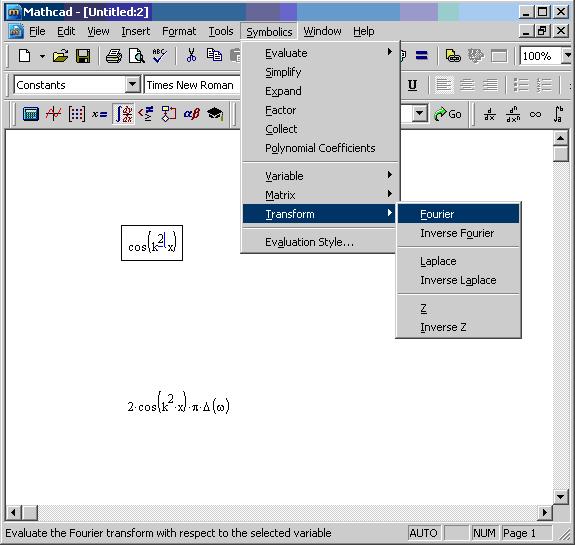
Рис. 1. Расчет Фурье-преобразования при помощи меню
Преобразованием Лапласа называют интеграл от f (х) следующего вида:
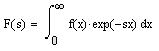
Рассчитывается преобразование Лапласа совершенно аналогично Фурье-преобразованию. Пример преобразования Лапласа приведен на рис. 2.

Рис. 2. Двумерное преобразование Лапласа:
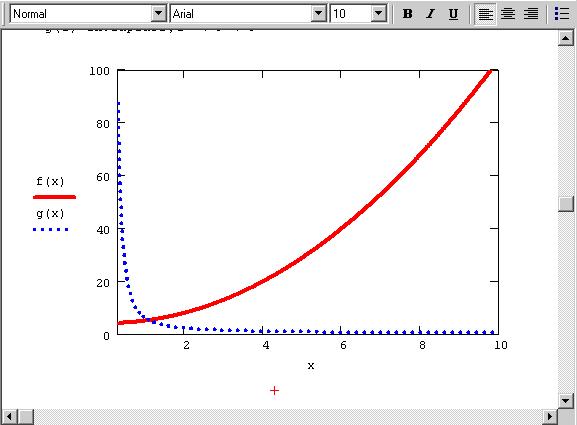
Рис. 3. Прямое и обратное преобразование Лапласа (продолжение рис.2)
Z-преобразование (Z) функции f (х) определяется не интегралом, а бесконечной суммой следующего вида:
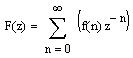
Пример Z-преобразования приведен на рис. 4, а его результаты — на рис. 5.
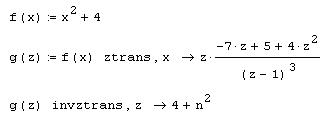
Рис. 3. Прямое и обратное Z-преобразование
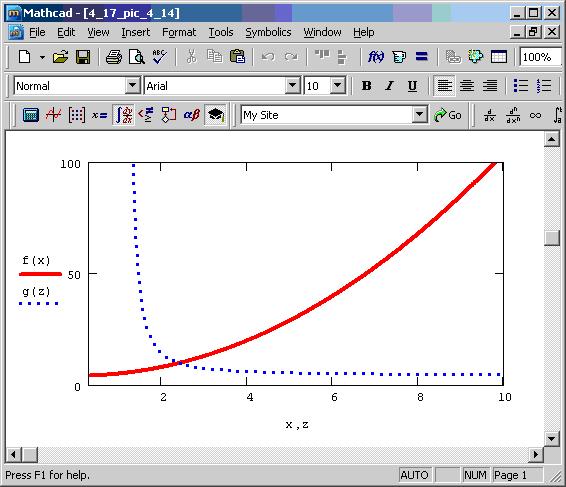
Рис. 5. Прямое и обратное Z-преобразование (продолжение рис. 4)
Выполнила Плеханова Юлия
|
