Меню Символика (Symbolics) Mathcad. Пункт Переменная (Variable)
вернуться на главную страницу можно, воспользовавшись ссылкой.

Меню Symbolics (Символьные вычисления) содержит операции символьной математики. В пункте Variable (переменная) объединены операции математического анализа:

Если в рабочем документе в некотором выражении выделена переменная, то после щелчка по соответствующей строке меню в рабочем документе отображается результат выполнения операции относительно выделенной переменной.

Решение уравнений (Solve)

С помощью символьного процессора можно вычислить аналитически значение переменной, при котором выражение обращается в ноль. Для этого:

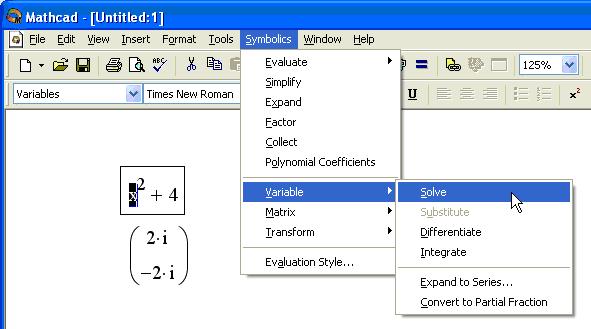
Рис. 1. Символьное решение уравнения

Подстановка переменной (Substitute)

Очень удобная возможность символьных вычислений — это операция подстановки значения переменной в выражение. При помощи меню подстановка производится следующим образом (рис. 2):

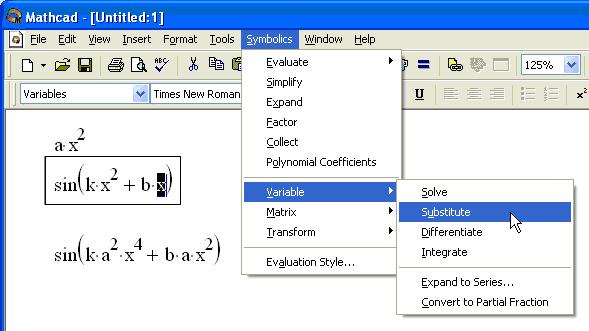
Рис. 2. Подстановка значения переменной

Для осуществления той же операции в совокупности с оператором символьного вывода используйте ключевое слово substitute, которое вставляется в документ одноименной кнопкой на панели Symbolic (Символика). После ключевого слова substitute необходимо ввести в место заполнители логическое выражение, показывающее, какую именно переменную какой формулой следует заменить.

Дифференцирование (Differentiate)

Чтобы аналитически продифференцировать выражение по некоторой переменной, необходимо выделить в нем эту переменную и выберать команду Symbolics / Variable /Differentiate (Символика/ Переменная /Дифференцировать) (рис. 3).

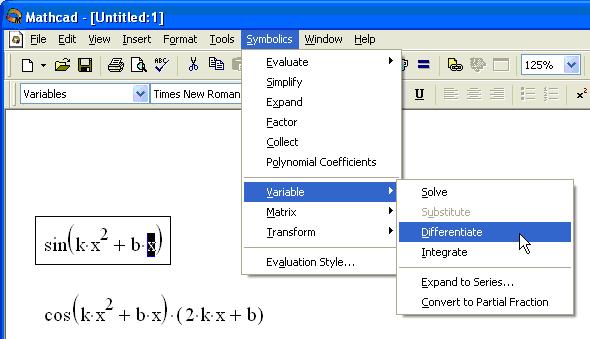
Рис. 3. Дифференцирование по переменной

В результате в следующей строке за выражением появится значение ее производной. Для того чтобы найти вторую производную, повторно примените эту последовательность действий, но уже к полученному результату дифференцирования. Так же находятся и производные высших порядков.

Интегрирование (Integrate)

Для вычисления неопределенного интеграла от некоторого выражения по определенной переменной необходимо выделить в выражении переменную и выполнить команду Symbolics / Variable / Integrate (Символика / Переменная / Интегрировать) (рис. 4). Вычисленное аналитическое представление неопределенного интеграла появится ниже. При этом результат может содержать как встроенные в Mathcad функции, так и другие спецфункции, которые нельзя непосредственно рассчитать в Mathcad, но символьный процессор "умеет" выдавать их в качестве результата некоторых символьных операций.

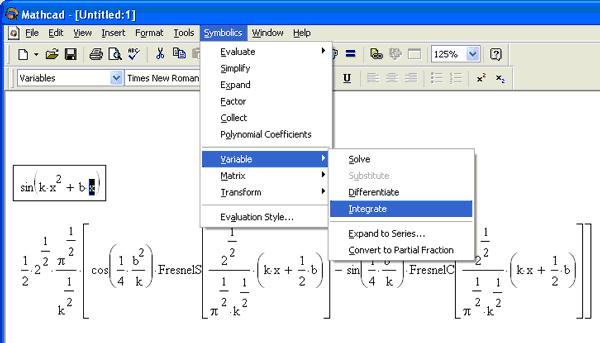
Рис. 4. Интегрирование по переменной

Разложение в ряд (Expand to Series)

С помощью символьного процессора Mathcad возможно получить разложение выражения в ряд Тейлора по любой переменной х в точке х=о, т. е. представить выражение в окрестности точки х суммой вида a0+a1x+a2x2+a3x3+... Здесь а1— некоторые коэффициенты, не зависящие от х, но, возможно, являющиеся функциями других переменных, входящих в исходное выражение. Если выражение имеет в точке х=о особенность, то * соответствующее разложение называют рядом Лорана.

Чтобы разложить выражение в ряд

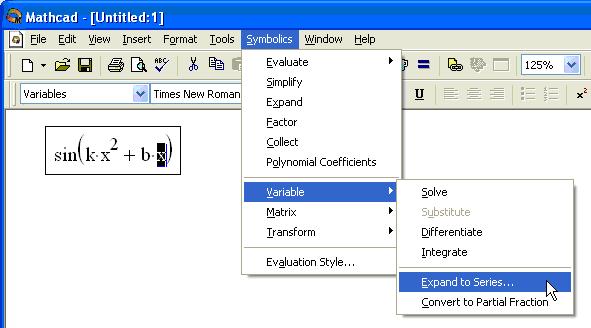
Рис. 5. Подготовка выражения для разложения в ряд по переменной х

Разложение на элементарные дроби (Convert to Partial Fractions)

Чтобы разложить сложную дробь на более простые дроби, следует либо выполнить команду Symbolics / Variable / Convert to Partial Fractions (Символика / Переменная / Разложить на элементарные дроби) (рис. 6), либо указать ключевое слово parfrас. Применяя первый способ (меню), необходимо перед выбором его команды выделить переменную, по которой будет производиться разложение, а если используется второй способ (с оператором символьного вывода), то имя переменной следует указать после ключевого слова parfгас.

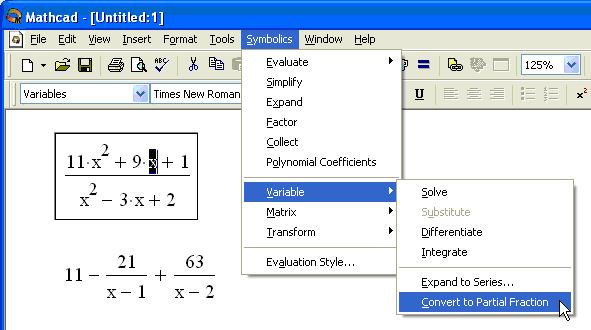
Рис. 6. Разложение сложной дроби на элементарные дроби

Выполнила Омельченко Светлана