|
Если возникли проблемы при выполнении Задания 4.
вернуться на главную страницу можно, воспользовавшись ссылкой.
Коллеги, Подробности выполнения Задания 2.11 с данными реального МОБ Республики Беларусь, в том случае, если оно не получается, будут доступны позже. В случае проблем с этим заданием, вынесите недоделанный вариант в отдельный файл Mathcad и в его назовании замените номер задания ("4") на "MOB".
2.14. Проверьте, пожалуйста, условие, при котором заданная матрица является структурной матрицей внешней торговли (см. стр. 131), и в том случае, если оно не вополняется - скорректируете последний элемент соответствующего столбца на нужную величину. При этом если исходный элемент равен x, а корректирующая величина равна y, запишите в соответствующей ячейке резултат как разность x-у или сумму x+y, а не полученное число.
2.16. Многие варианты исходных данных дают очень парадоксальные результаты.
Во-первых, матрица АTA может быть необратима. В этом случае остается, проверив исходные данные, просто констатировать этот факт, а также то, что по предложенному способу мы не можем вычислить нормальное обобщенное решение системы. Вместе с тем, и в этом случае рекомендую проверить, можем ли мы найти классическое решение систем.
Во-вторых, обе невязки могут быть отличными от нуля, то есть следуя логике, мы должны сделать вывод о несовместности обеих систем, однако классическое решение для одной из них, тем не менее, легко можно найти (см. ниже - невязка в системе для найденного по формуле нормального обобщенного решения равна 15,759, и это при наличии классического решения).
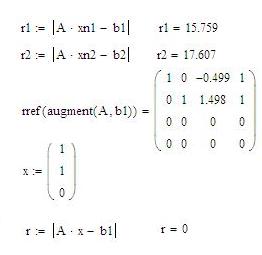
Итак, невязка найденного по формуле (ATA)^-1ATb нормального обобщенного решения совместной системы уравнений может быть отлична от нуля. Очевидно, что происходит это потому, что матрица АTA является плохо обусловленной, т.е. незначительные изменения ее элементов (например, погрешности округления) приводят к значительным изменениям обратной к ней матрицы.
Сделайте, в этом случае, соответствующий вывод.
Важное дополнение. Уважаемые коллеги, в связи с многочисленными вопросами, возникла необходимость уточнить: в поиске классического решения в данном случае Mathcad лишь помогает, но не находит его. Функции программы заканчиваются на том, что с помощью функции rref() она приводит матрицу A и вектор b к ступенчатому виду. И далее вы уже сами находите вектор x, решая уравнение (коэффициенты при трех иксах - x1, x2 и x3 - элементы матрицы А, только в ступенчатом виде, а правые части - вектор b) относительно трех переменных. И затем сами присваиваете вектору x найденное значение (х:=).
Например, в данном случае у системы может быть множество решений - x3, вообще говоря, может быть любым, а x1 и x2 можно, соответственно, выразить через x3 (ранг матрицы, как видите, равен 2) и для системы, соответственно, можно записать т.н. общее решение, а затем и фундаментальное.
В т.ч. одним из решений - наиболее, как представляется, простым, является представленное на экране. Для того, чтобы найти его, сначала возьмем x3=0, а затем, подставив его в первое и второе уравнения найдем x1 (из уравнения 1*х1+0*Х2-0.499*х3=1 или x1=1) и х2 (из уравнения 0*X1+1*x2+1,498*0=1 или x2=1)...
|
